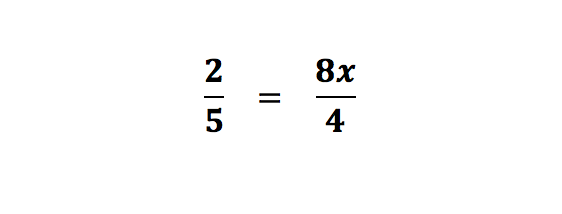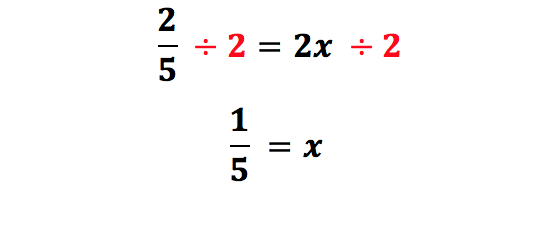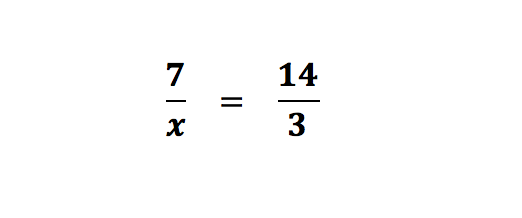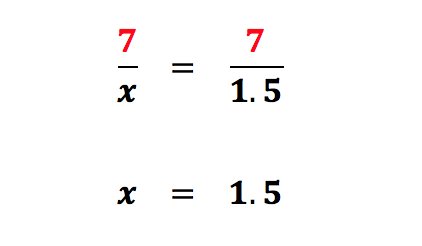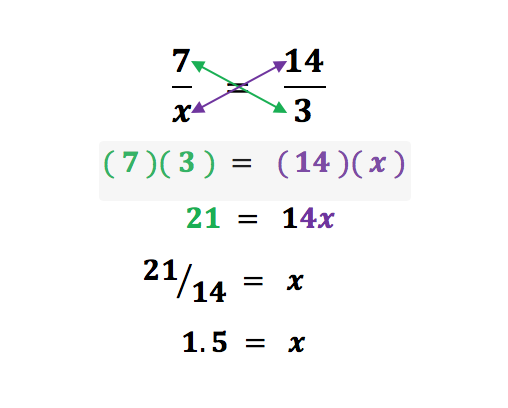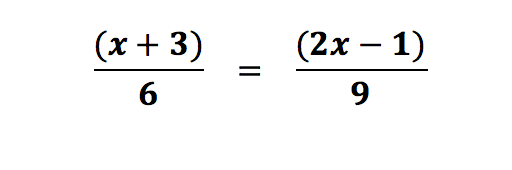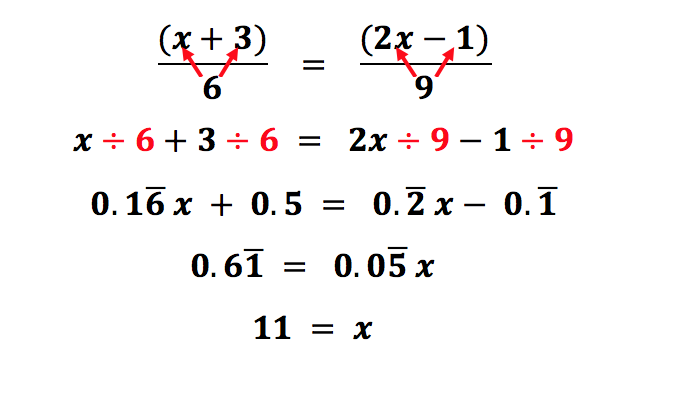Tips from an Anaheim Math Tutor: Should You “Cross Multiply”?


“Cross multiply” is an often-used term in mathematics that often sticks in people’s memories long after they graduate high school and stop taking math classes. However, most of those people don’t really know what it is and why it works. So many students are just taught to “cross multiply” when they see an equation with fractions. Unlike many other memorized phrases in math, cross multiplication is actually a useful tool that often makes problems with fractions a little bit easier – sign up for your private Anaheim math tutor.
But just like anything else you memorize in math, you should understand what you’re doing rather than just memorizing a seemingly arbitrary procedure. Cross multiplication is just the “undoing” of division that is being done. If you have two fractions, that is the same as dividing by something on each side. And, just like we can subtract to “undo” addition, we can multiply to “undo” the division that is making those pesky fractions.
Here are three examples that we will solve both with and without cross multiplying. You can see that there are always other ways to solve these problems, as well as why cross multiplying works and is a little bit simpler.
As a general rule of thumb, I do not teach cross multiplication without making sure my students know how to solve the problems without it first. That way I help promote a stronger understanding of how to solve simple algebraic equations that will hopefully stick with them and translate to other math skills rather than leaving them thinking “cross multiply is how you have to solve fractions.”
Here is the first example:
In this example, we have two fractions and need to solve for x. To help find x, we can notice that the fraction on the right can be reduced:
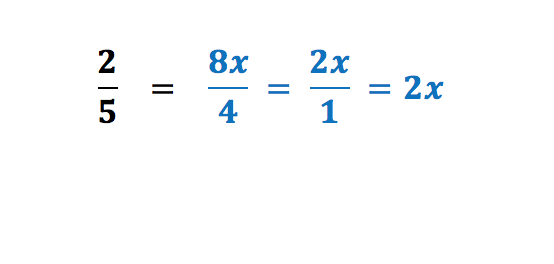
We get a solution of one fifth (1/5) which is equal to 0.2. No cross multiplying was needed, only our standard multiplication and division. Let’s do the same with cross multiplication:
Here, we didn’t think about reducing the initial fraction. We simply cross multiplied: taking the diagonal terms in our fractions and multiplying them together (one set in green and the other in purple). This makes the “cross” of our cross multiplication. After we do this, we get a fairly trivial equation of 8 = 40x to solved. We divide both sides by 40 and get the same answer we did above.
Example 2:
Now the x is on the bottom of the fraction. To solve this, we could multiply both sides by x to “undo” the 7 being divided by an x on the left. However, another way would be to make the right side of the equation look like the left. We notice that the left side has a 7 on top, but the right side has a 14. We can change the 14 into a 7 by halving the top and bottom of the right:
Let’s use cross multiplication to solve the same problem:
No extra thinking here or even trying to get the x out of the bottom of the fraction. We simply follow the cross multiplying procedure and multiply the green together and the purples to get our final, simple equation that yields the same 1.5 answer.
Example 3:
Our last example gets a little more complex with terms in parentheses. Cross multiplying here would probably be the best choice, but it’s never the only choice. The fraction on the left is a term being divided by 6. The fraction on the right is a term being divided by 9. We can distribute the division (just like you would distribute multiplication into parentheses) to get an equation we can solve:
We could have kept our work as fractions instead of decimals, but this is likely how it would look if you were using a calculator to help you solve the problem, and decimals are equally as valid as long as we don’t round them. Let’s see how it looks using cross multiplication:
Here we get the same answer as above by following the exact same cross multiplication procedure. Notice that we still had to distribute when we multiplied the terms in parentheses.
Cross multiplying can be a very helpful tool when solving equations with fractions. However, it should not be thought of as the only way to do so, and it should not be the only way students are taught. Thinking this way will continue to lead to many students being confused about fractions and unsure of how to work with them. Cross multiply doesn’t have to go away, but the blind memorization of it should.
replace logoAll blog entries, with the exception of guest bloggers, are
100% Satisfaction Guarantee
You’ll love your tutor, or you don’t pay.

We will evaluate your situation and answer any questions. We will then individually match you with one of our tutors. Your tutor will recommend the best strategies for you based on your goals. You’ll work with the same tutor ongoing and you can schedule directly with your tutor.
100% Satisfaction Guarantee – You’ll love your tutor, or you don’t pay
| Cookie | Duration | Description |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |