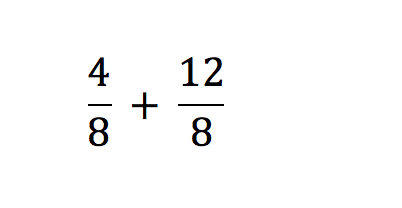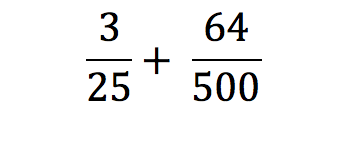Anaheim Math Tutor Tips: Solve Fractions With a Simple Calculator


Even if you don’t have access to a graphing or scientific calculator, you can still check fractions with a much simpler calculator. This can be relevant if you are using your phone, taking a test where your teacher supplies only simple calculators, or taking an online standardized test like the GRE where you only have an onscreen simple calculator.
Many students do not realize it is still possible to work with fractions with these types of calculators. It’s true that fractions likely won’t be nearly as easy to use on these options, and there is a good chance you will have to do some calculations by hand. However, they are still a valuable tool to check your answers and solve some fraction problems. First, let’s show some examples of simple calculators and then work through examples of how to use fractions with them (book your in-home Anaheim math tutor today).
A Casio brand of a simple calculator with little extra functionality outside of addition, subtraction, multiplication, and division but with extra finance related options.
A Karuida brand calculator similar to the Casio that is also very common.
An example of a simple phone calculator. Many phones may also have more calculator options on their stock apps (as well as the ability to download different calculator applications with more functionality), but this is an example of the few options that may be readily present.
This is an example of an onscreen calculator that you may get for a computer-based test. Specifically, this is the current calculator available on the GRE
Here is a keychain or pocket calculator with no functionality outside of basic operations.
We can now practice some examples of how to work with fractions using these types of calculators. First, the most important fact to know is that the division function is how we can get access to fractions. A division sign is the same basic function as a fraction bar – that is, to get 3/5 you would need to type 3 ÷ 5. It is important, however, to do as few calculations at once on simple calculators. Many will follow the order of operations, but others will just give you an immediate output from your first operation. For example, to find 47-19/4 you would want to perform the 47 – 19 first and separately, then divide that answer by 4.
Example 1:
Here, we can input each of the fractions into the calculator first to get the outputs in decimal form. We put into the calculator the first fraction as 4 ÷ 8. The output we get is 0.5. Next, we input the second fraction as 12 ÷ 8 and receive the output of 1.5. Now we have converted both fractions into decimals and can add them as 0.5 + 1.5 to get the correct answer of 2.
Example 2:
Now, let’s try the same strategy as example 1. We input the first fraction as 9 ÷ 4. The output we receive on our simple calculator is 2.25. We then input the next fraction as 1 ÷ 6 to get 0.16667 or some similar number. We can now type these into the calculator as 2.25 – 0.166667 to get an answer of 2.08333. However, this likely isn’t the answer we want, since it isn’t a fraction or full number.
Unfortunately, there is no easy way around this problem without at least some knowledge of fraction manipulation. The first option is to find a common denominator and subtract. A quick way to do this is to multiple each fraction on the top and bottom by the denominator (bottom) of the other fraction. So, we multiply the first fraction by 6/6 and the second fraction by 4/4. This will change our fractions now to 54/24 – 4/24 . Now we have a common denominator and can just subtract the numerators of each (54 – 4) to get a final answer of 50/24. Finally, we can reduce this by dividing the top and bottom by 2 to get 25/12.
Now we can get to the calculator part. Input 25 ÷ 12 into a calculator and you get this result: 2.08333. Notice that this is the same answer as when we worked with strictly decimals. However, the decimal version took a lot few steps and was quick to find. By doing this, we can essentially check our answers to make sure they are correct. Complete the fraction operation by hand and find your answer as a fraction. Then, convert it to a decimal in the calculator and find the decimal using just the calculator and compare answers. If they aren’t the same, you likely made a mistake in your fraction operations.
Example 3:
With this example, let’s try to solve it just in the calculator. We input the first fraction as 3 ÷ 25 to get 0.12 and the second fraction as 64 ÷ 500 to get 0.128. Now we can add those two together: 0.12 + 0128 to get a final decimal of 0.248.
In the last example, we were stuck with the decimal and could only use it to check our answer. Here, however, we can notice that the decimal “terminates” quickly, or it stops after just a few digits. Using this, we can write any terminating decimal as a fraction based on the furthest decimal place it has. 0.5 we could write as 5/10. 0.14 we could write as 14/100. And 0.027 we could write as 27/1000. Following this trend, we could write 0.248 as 248/1000. This is a fraction that we can then reduce to have the simplest answer: 31/125 after dividing the top and bottom by 8.
So, we can use even the simplest of calculators to solve fraction problems. At best, you may need zero knowledge of how to solve fractions (example 1), and at worst, you will have to solve the problem normally but be able to check your answer (example 2). There is also a good chance you will only need minimal fraction reducing knowledge (example 3). Regardless of the situation, you should know how to use calculators to check your answers and solve problems – even when you don’t have a fancy calculator available.
Book your private Anaheim math tutor today.
Michael C. is currently a private math, science, and standardized test tutor with TutorNerds in Irvine and Anaheim.
100% Satisfaction Guarantee
You’ll love your tutor, or you don’t pay.

We will evaluate your situation and answer any questions. We will then individually match you with one of our tutors. Your tutor will recommend the best strategies for you based on your goals. You’ll work with the same tutor ongoing and you can schedule directly with your tutor.
100% Satisfaction Guarantee – You’ll love your tutor, or you don’t pay
| Cookie | Duration | Description |
|---|---|---|
| cookielawinfo-checkbox-analytics | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics". |
| cookielawinfo-checkbox-functional | 11 months | The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". |
| cookielawinfo-checkbox-necessary | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". |
| cookielawinfo-checkbox-others | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other. |
| cookielawinfo-checkbox-performance | 11 months | This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance". |
| viewed_cookie_policy | 11 months | The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data. |